Python递归和生成器实现斐波那契数列区别

前言

斐波那契数列，又称黄金分割数列，又名兔子数列。

通俗的来说，即从该数列中的第三项开始，后面的每一个数的值等于前两个数的和。

而我们通过 python 如何来实现不同长度的斐波那契数列呢？
常见的实现方法有递归和生成器。

那么小编今天就为大家介绍用这两种方式实现斐波那契数列的区别。

推荐阅读：Python3 入门、Python3 进阶

递归

递归的方法效率较低，会出现大量重复计算，这里以 20 个斐波那契数列为例。

def fbnq_one(self): 
    if self == 1: 
        return 1 
    elif self == 2: 
        return 2 
    else: 
        return fbnq_one(self - 2) + fbnq_one(self - 1) 
print([fbnq_one(i) for i in range(1, 21)])

生成器

生成器需要在方法中运用 yield，生成器是一个可迭代对象，可以遍历获取元素，在获取较多斐波那契数列时，相比递归效率较高，这里以 100 个斐波那契数列为例。

def fbnq_two(max_num): 
    a, b = 0, 1 
    time_num = 0 
    while time_num < max_num: 
        yield a 
        a, b = b, a+b 
        time_num += 1 
print([i for i in fbnq_two(100)])

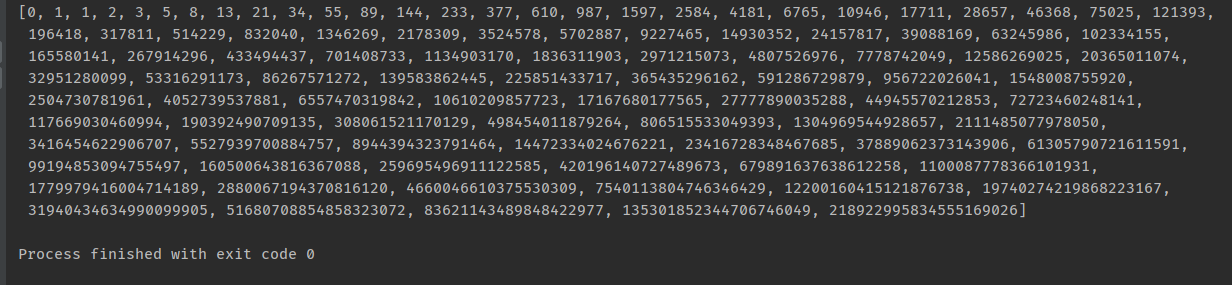
比较

递归语法简单，但执行起来，重复计算多，数值一大，运行时间就变长；
生成器可以遍历获取元素，在获取较多斐波那契数列时，相比递归效率较高，运行时间相对更快。